Wordle Pangrams
It all started with my friend Tim watching this video by Matt Parker
The problem Matt was trying to solve was to find 5 5-letter words (as in the Wordle dictionary) that between them contained 25 different letters of the alphabet, i.e. none of the five words had any letters in common.
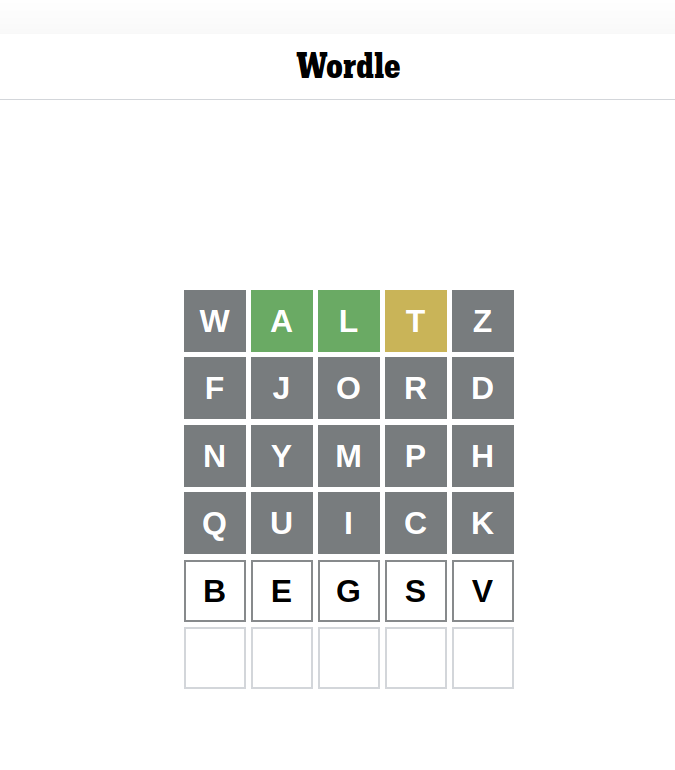
I sat and thought for a while and came up with - 24 letters with WALTZ, FJORD, NYMPH, QUICK, and BEGS - close but no cigar, as the saying goes. Time to write some code. I'd not seen the video at the time so didn't know that Matt had written some code that took almost two months to run. I set myself a target of under an hour (on my 12 year old first gen i7 desktop).
The problem space is huge, there are 12972 words in the original, pre-NY Times and so there are 12972*12971*12970*12969*12968/120 different combinations - that's 3,058,571,387,612,503,040 which might take more than an hour (more than a year, more than a decade...) to work out and check all of them.
One way to reduce that is to ignore all the words that have two or more of the same letter in them - they automatically exclude themselves from the solution. Removing them reduces the list size to a mere 8322 words. But we can go one stage further and remove all the anagrams of the remaining words (remembering them so if any are in the solution we can add in the extra anagram versions of the solution). Amazingly that drops the word count to 5182.
Now that seems like a huge reduction, over 50% but simply checking every combination would require 5182*5181*5180*5179*5178/120 =310,190,561,767,076,760 which is still a HUGE number. Checking every combination simply won't work.
I spent a long time thinking about how to loop over the combinations breaking out of the loops immediately I found a fail, but my brain simply wasn't big enough to work out the complex code. Even worse, a natural solution might involve recursion. To be honest I stalled, but a chance conversation down the pub with another friend, Charlie and he sent me a list of solutions the following day - done using a spreadsheet! Amazing!
Then I had an idea, rather than stop iterating every time there was a clash, why not filter the iterations so that clashes could never happen. So the first iteration I would iterate all the way through the entire 5182 words but for each word (word1, say) I would then build a list of all words that didn't have any common letters and iterate through this (word2) say to build a list of word3 letters and if this existed I'd build a list of word 4 letters (this list wouldn't happen too often and would likely be quite small). If I did have a word4 list (i.e. words that had no letters in common with word1, word2, word3, and word4 then I'd try and build a list of any words that also had nothing in common with any of these. The rare occasion this word5 list actually succeeded then word1, word2, word3, word4, and any word5s would be the solution to the problem.
This approach is very Pythonic too as Python's list comprehension makes building the filtered lists pretty trivial. There were some further optimisations, the main one being that if I'm some way down that 5182 long list of word1 words I need only start building the word2 list from the next word (e.g. if I'm at 100 words down the original 5182 word list for word1, I can start filtering the word 2 list at word 101). Why? Lets take the 20th word as an example. If I compare the 100th word in the list as word1 and the 20th word in the list as word2 that's exactly the same as comparing the 20th word in the list as word1 with the 100th word in the list as word2 - which I've already done. There's also a very minor tweak that means I can cut the word1 list 4 words (i.e. at 5178) before the end, the word2 list 3 words before the end, etc.
Assuming the filtering is fast (it is) then the number of iterations shrinks dramatically. That list of word2 words is generally a fraction of the original 5182 and the word3 list is much, much, smaller. If any word4s exist at all they will be pretty scarce and, on the 10 occasions we actually have a list of word5s then it is a list of length 1! The problem with this approach is that, since the filtered word lists are being built dynamically it is not possible to calculate their length in advance, and so work out how many iterations the code might take. So I had to temporarily add some counts and was somewhat amazed that this approach takes just 63,515,889 - a relatively small number, especially when compared to 3,729,483,737,997,660,720
A real life example, I set the debugger to break at word 2000 out of the 5182 words, which happened to be 'carts'. So the second list of words will be all the words from position 2001 to the end of the list (i.e. 2182 of them) but filtered to exclude any with any of the letters 'c', 'a', 'r', 't', or 's' - this reduces that 2182 to just 413 words to check. The first of these happened to be at the first position in the 413 words list and was 'defog'. So now we check the 412 words in the list from position 2 to the end - but exclude any with letters in 'defog' (we don't need to exclude any 'carts' letters this time as they've already been filtered). Filtering the 412 words leads to just 27 words in the third list to check, and the first 7 of these meant that no further 4th words could be found, but the 8th in the list 'jumby' did give a couple of options for word 4 - 'plink' and 'whilk'. But neither of those lead to a fifth word and solution.
The next thing was to optimise the code, even just 63 and a half million comparisons of 5 digit strings might take some time. So I converted each of those unique lettered, anagrams removed words to 26 bit binary number - simply if there was an 'a' in the word then bit 25 would be set, a 'b' meant bit 24 ... and a 'z' bit 0. Now working with these, comparing two is simply a Boolean AND and if that result is 0 the binary numbers have no bits in common, i.e. the original words have no letters in common - Boolean ANDs tend to be very fast computer operations.
Here's the algorithm:
answers = []
# Get first candidate word (bword0) by interating through the entire list
# Note - don't need last 4 words, they will be checked in the later iterations
for i1, bword1 in enumerate(binwords1[:-4]): # Binwords1 is the entire list of words
# For each word in the forst word list build the second word list,
# starting at the current position in the list + 1
# but filtering out all words that have any letters in common with bword1
# and then iterate through this list of second words (bword2)
binwords2 = [bw for bw in binwords1[i1 + 1:] if not (bw & bword1)]
if binwords2: # The code works without checking that the list exists but the check optimises the code slightly!
for i2, bword2 in enumerate(binwords2[:-3]): # Again, last 3 words will be checked later
# Build a third word list in a similar fashion and iterate through
# Note since the list binword2 is filtered not to contain bits common with bword1 we need only check ...
# commonality with bword2 (i.e. no need to accumulate a bitmap for all previous words to check against)
binwords3 = [bw for bw in binwords2[i2 + 1:] if not (bw & bword2)]
if binwords3:
for i3, bword3 in enumerate(binwords3[:-2]):
# Now try to build a fourth wordlist of words with letters not in words1, 2, and 3
binwords4 = [bw for bw in binwords3[i3 + 1:] if not (bw & bword3)]
if binwords4:
for i4, bword4 in enumerate(binwords4[:-1]):
# We have 4 words - try and build a list of 5th words that don't have letter matches
# If this list is non-empty we have solutions!
binwords5 = [bw for bw in binwords4[i4 + 1:] if not (bw & bword4)]
if binwords5:
for bword5 in binwords5:
answers.append([bword1, bword2, bword3, bword4, bword5])
return answers # List of all the possible Wordle Pangrams (excluding anagrams)
The above code certainly shows the power of Python list comprehension and slicing in the one-liner for building the filtered lists.
binwords2 = [bw for bw in binwords1[i1 + 1:] if not (bw & bword1)]
And that's about it. There's obviously some code to remove words with duplicate letters - but again Python helps :
if len(set(aword)) == len(aword)is a simple check for words of all unique letters and, of course, converting the words to binary numbers makes detecting anagrams as simple as checking the binary number is unique. There's also some horrible kludge code to scan the solutions checking if any of the words are anagrams and, if so, creating new, alternative solutions. Believe it or not, one of the words in one of the solutions actually has an anagram!
Oh, if you are interested - here's the complete list of Wordle Pangrams:
fjord, nymph, waltz, gucks, vibex
fjord, chunk, waltz, gymps, vibex
prick, glent, jumby, vozhd, waqfs
brick, jumpy, glent, vozhd, waqfs
jumpy, bling, treck, vozhd, waqfs
bemix, clunk, grypt, vozhd, waqfs
blunk, cimex, grypt, vozhd, waqfs
brung, cylix, kempt, vozhd, waqfs
brung, xylic, kempt, vozhd, waqfs
clipt, jumby, kreng, vozhd, waqfs
jumby, pling, treck, vozhd, waqfs
Oh, yes, I also forgot - how long does this code take? Well on my 12 year old i7 it takes 2 mins 20 secs - I beat my hour target by a margin that surprised even me. It's almost a minute longer on my MacBook Air which shows my aging Linux desktop is still a pretty good development machine!
Here's the complete code:
import WordleDict
import string
import time
def time_usage(func):
"""
Simple decorator function to calculate and print time taken for any function
"""
def wrapper(*args, **kwargs):
begin_ts = time.time()
retval = func(*args, **kwargs)
end_ts = time.time()
print(F"Function - {func.__name__}: Elapsed time: {(end_ts - begin_ts)}")
return retval
return wrapper
def binariseword(word):
"""
Convert any word into 26-bit bitmap a=bit25 set, b= bit24 et .. z = bit 0 set
NOTE - although this was written for 5 char Wordle words, it will work withwords of any length and either ...
Upper or Lowr case, or a mix thereof
:param word: A character string containing alphabetic only characters
:return bitmap: the binary representation of the word
"""
bitmap = 0
for letter in word.lower():
bit = 1 << string.ascii_lowercase.index(letter) # Set the bit depending on position of letter in alphabet
bitmap = bitmap | bit # and accumulate into a bitmap of all letters in the word
return bitmap
# @time_usage
def uniqueletters_noanagrams_bin(wordlist):
"""
Filter a list of words removing any words that contain duplicate letters and or anagrams
Also convert any such words to a binary bitmap equivalent (see binarise word)
:param wordlist: list of character string words
:return bwdict: A dictionary of with the filtered binarised words as keys with the char equivalent values
:return anagdict: A dictionary of binarised words with an array of anagrams - the word as in bwdict is the first
element in this array - this is only created if there are actually anagrams
"""
# Should be separate functions but for a large wordlist combining into one saves an iteration
bwdict = {}
anagdict = {}
bitset = set()
for word in wordlist:
# Is the set of unique letters in the word the same length as the number of letters in the word?
if len(set(word)) == len(word): # If so the word doesn't have duplicate letters
bitmap = binariseword(word) # so convert the word to its binary bitmap equivalent
# Does the set of bitmaps so far contain this bitmap
if bitmap not in bitset: # No - so it is not an anagram of an existing word (which would have same bitmap)
bwdict[bitmap] = word
bitset.add(bitmap) # and the the new binarised word into the set of all such so far
else: # Yes - we already have this bitmap so the word is an anagram of an existing word
if bitmap not in anagdict: # Do we already have other anagrams of the word?
anagdict[bitmap] = [bwdict[bitmap],
word] # No - create a dictionary entry for the original word ...
else: # Yes - add it to the existling list of anagrams ... and its newly found anagram
anagdict[bitmap].append(word)
return bwdict, anagdict
@time_usage
def get_pangrams(binwords1):
"""
Find all five word panagrams in the list of 5 letter Wordle words (which have been binarised)
- i.e. a set of words comprising 25 distinct letters (or 25 distinct bits in the binarised version)
:param binwords: A list of binarised words to search and check for pangrams
:return answers: A list of 5 entry lists containing binarised words that comprise the pangram
"""
# This module is the core of this code and finding an efficient algorithm is necessary
# There are 12972 words in the Wordle list (original version pre-NY Times). After filtering out words with ...
# duplicate letters this is still 5182 unique character strings. So there are are 5182!/5177! or ...
# 3.7359635e+18 total combinations!!
# This code reduces the iterations substantially (to just 74582079 iterations)
# It iterates through the entire list of words and for each word produces a (smaller) filtered list of all ...
# words which do not share common letters with that word. It then iterates through this list for the second word ...
# and for each second word it produces a (now much smaller) list of filtered third words, For each word in this ...
# third list a fourth word list of all words not sharing letters with words1, 2 or 3 is produced ...
# (if any such exist) and should iterating this produce any list of fifth words we have a solution!
# The iteration loop for the second word need only start after the current position of the current initial word ...
# iteration e.g. if we are at iteration 100 in word 0 we can start building the filtered list for the second ...
# word starting at position 101. This is (again for example) word 10 on the second iteration compared with word ...
# 100 on the first iteration is the same as word 10 on the first iteration compared with word 100 on the second ...
# which has already been checked.
# The code is further optimised by using the binarised equivalent version of the words so a simply Boolean AND ...
# suffices to check commonality of bits (i.e. letters in the original word)
answers = []
# Get first candidate word (bword0) by interating through the entire list
# Note - don't need last 4 words, they will be checked in the later iterations
for i1, bword1 in enumerate(binwords1[:-4]): # Binwords1 is the entire list of words
# For each word in the forst word list build the second word list,
# starting at the current position in the list + 1
# but filtering out all words that have any letters in common with bword1
# and then iterate through this list of second words (bword2)
binwords2 = [bw for bw in binwords1[i1 + 1:] if not (bw & bword1)]
if binwords2: # The code works without checking that the list exists but the check optimises the code slightly!
for i2, bword2 in enumerate(binwords2[:-3]): # Again, last 3 words will be checked later
# Build a third word list in a similar fashion and iterate through
# Note since the list binword2 is filtered not to contain bits common with bword1 we need only check ...
# commonality with bword2 (i.e. no need to accumulate a bitmap for all previous words to check against)
binwords3 = [bw for bw in binwords2[i2 + 1:] if not (bw & bword2)]
if binwords3:
for i3, bword3 in enumerate(binwords3[:-2]):
# Now try to build a fourth wordlist of words with letters not in words1, 2, and 3
binwords4 = [bw for bw in binwords3[i3 + 1:] if not (bw & bword3)]
if binwords4:
for i4, bword4 in enumerate(binwords4[:-1]):
# We have 4 words - try and build a list of 5th words that don't have letter matches
# If this list is non-empty we have solutions!
binwords5 = [bw for bw in binwords4[i4 + 1:] if not (bw & bword4)]
if binwords5:
for bword5 in binwords5:
answers.append([bword1, bword2, bword3, bword4, bword5])
return answers
# @time_usage
def print_with_angrams(bw_solutions, anagdict):
"""
Print all the pangram solutions including all anagram variants
:param bw_solutions: A list of lists of 5 letter binarised word pangrams
:param anagdict: A dictionary mapping the binarised word to all anagrams thereof
:return NONE:
"""
# This is horrible KLUDGE code. Converting the binarised word lists to words and printing is trivial but ...
# folding in all anagrams is horrible, especially since more than one word in a solution may have one or more ...
# anagrams
solutions = []
for bw_solution in bw_solutions: # Get a single binary solution
solution = []
for bword in bw_solution:
solution.append(bwdict[bword]) # Convert the binarised word back to its char equivalent
solutions.append(solution) # and add the list of char pangrams into a total solutions list
for bword in bw_solution:
if bword in anagdict: # iterate through the binarised words again looking for anagrams
for i in range(len(anagdict[bword]) - 1): # there may be more than one so need to iterate anagrams
oldword = anagdict[bword][i] # get the original word, or previous anagram
newword = anagdict[bword][i + 1] # and get its newly found anagram
for oldsolution in solutions: # go back through all the existing lists of pangrams
if oldword in oldsolution: # and if the old word is in the list replace it with the new
newsolution = list(map(lambda x: x.replace(oldword, newword), oldsolution))
solutions.append(newsolution) # dynamically extend the list of solutions so if other ...
# words in this pangram are anagrammed all combinations ...
# will be produced.
for solution in solutions: # Now simply print all the solutions which now includes all anagram variants
print(', '.join([word for word in solution]))
# END OF THE FUNCTIONS - MAIN CODE STARTS HERE
if __name__ == "__main__":
bwdict, anagdict = uniqueletters_noanagrams_bin(WordleDict.all) # Filter out anagrams and duplicate letter words
solutions = get_pangrams(list(bwdict.keys())) # Use the binary equivalents of the words to find all pangrams
print_with_angrams(solutions, anagdict) # Print the solutions along with any anagram variants